A comparação e selecção de fundos de investimento é um exercício complexo, dada a enorme oferta de produtos existente no mercado. Com efeito, várias dimensões deverão ser consideradas, como a conjuntura macroeconómica, as perspectivas para o mercado ou sector em causa, e a comparação e selecção de alternativas. Relativamente a esta última, várias são as ferramentas disponíveis, destacando-se as seguintes:
ÍNDICE DE SHARPE
Mede a relação entre (1) a rendibilidade obtida pelo fundo, em excesso face a uma aplicação sem risco, e (2) o risco assumido, medido pela respectiva volatilidade. O Índice de Sharpe é usado como medida de qualidade da rendibilidade do fundo, relacionando rendibilidade e risco: quanto maior o seu valor, maior a eficiência da gestão. Por exemplo, considerem-se duas alternativas de investimento: num determinado período, o fundo A e fundo B registaram uma rendibilidade anualizada de 15% e 13%, respectivamente, com uma volatilidade anualizada de 25% e 18%, respectivamente; Admitindo ainda, que no mesmo período, a taxa de juro média sem risco foi de 2%, conclui-se que o fundo B, apesar da menor rendibilidade obtida, foi o mais eficiente, com um índice de Sharpe de 0.61 contra os 0.52 do fundo A, tendo conseguido gerar mais rendibilidade, em excesso à taxa de juro sem risco, por unidade de risco assumido. Ou seja, sobretudo no caso de existência de várias alternativas de investimento comparáveis, o Índice de Sharpe constitui uma ferramenta útil para, numa primeira fase, filtrar as melhores. A fórmula de cálculo do Índice de Sharpe (IS) é a seguinte:
 |
, sendo Rp a rendibilidade anualizada do fundo (ou portfolio), Rf a taxa de juro sem risco média no período analisado, e δp o desvio-padrão anualizado (volatilidade) das taxas de rendibilidade. |
ÍNDICE DE TREYNOR
Índice de Treynor é outro dos indicadores utilizados na avaliação de duas ou mais alternativas de investimento. A fórmula de cálculo é semelhante à do Índice de Sharpe, com a diferença de que como medida de risco, no denominador, é utilizado o beta do portfolio, e não o desvio-padrão:
 |
, sendo βp o beta do portfolio (ver Risco Sistemático versus Risco Específico). |
A interpretação deste indicador é, igualmente, semelhante à do Índice de Sharpe. A diferença, e daí a sua utilização, reside na particularidade de incluir na análise o risco sistemático do portfolio (medido pelo indicador beta).
ÍNDICE DE SORTINO
O Índice de Sortino é mais uma ferramenta complementar ao Índice de Sharpe. Tal como este, mede a rendibilidade obtida por um portfolio, em excesso à taxa de juro sem risco, relativamente ao risco assumido. A diferença consiste na forma de aferição deste risco: ao contrário do Índice de Sharpe, que considera todos as taxas de rendibilidades históricas no cálculo do desvio-padrão, o Índice de Sortino é mais exigente e considera só, por exemplo, as taxas de rendibilidade negativas. Ou seja, considera apenas a volatilidade dos retornos negativos.
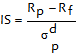 |
, sendo |
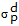 |
o desvio-padrão das taxas de rendibilidade negativas11 |
ALPHA DE JENSEN
O termo alpha deriva da estatística. Nos modelos de regressão linear simples, a equação que relaciona uma variável dependente y com outro qualquer factor x, é escrita como:
 |
O primeiro termo, α (alpha), representa a intercepção da recta com o eixo da variável dependente, β (beta) representa o declive dessa recta, e ε (epsilon) representa o resíduo ou erro aleatório. Em finanças, assume-se geralmente que as taxas de rendibilidade de um determinado activo têm uma relação linear com outro ou outros activos ou benchmarks de performance. O termo alpha é importante uma vez que representa a rendibilidade obtida pelos investidores no caso do benchmark registar uma rendibilidade nula. Assim, o alpha pode ser considerado como uma proxy da competência dos gestores de fundos.
Considerando-se Rp como a taxa de rendibilidade do fundo p, Rf como a taxa de juro sem risco e Rm como a taxa de rendibilidade do benchmark m, apresentam-se de seguida as formas de cálculo do alpha mais comuns (ignorando o termo residual ε).
| i) |
 |
A taxa de juro sem risco é considerada o benchmark do fundo. No entanto, tal só será correcto se a performance do fundo não for afectada por nenhum factor sistemático para além da taxa de juro sem risco, o que na prática só acontece para fundos de mercado monetário.
| ii) |
 |
Nesta forma de cálculo do alpha, o beta em relação ao benchmark é assumido igual a 1. A menos que a estratégia do fundo seja replicar a rendibilidade do benchmark, o alpha apurado desta forma é pouco ou nada significativo
| iii) |
 |
| com |
 |
Nesta forma, o beta deixa de ser assumido como igual a 1, e a taxa de juro sem risco continua a ser considerada nula. Embora mais correcta do ponto de vista financeiro, só deve ser usada se a rendibilidade do fundo não for afectada por mais nenhum factor de risco para além do considerado. Por outro lado, como se assume que a taxa de juro sem risco é zero, um fundo que utilize um leverage superior ao benchmark poderá indiciar um alpha positivo mesmo que tal não seja verdade. O alpha tem que ser superior a (1-β). Rf para que se possa afirmar uma performance superior quando ajustada pelo risco incorrido.
| iv) |
 |
Esta forma de cálculo, conhecida como Alpha de Jensen (1968) é a forma mais correcta de cálculo do alpha, sendo baseada no Capital Asset Pricing Model (CAPM):
 |
com |
 |
Por definição, quanto maior o alpha, maior a capacidade da gestão do fundo em adicionar rendibilidade não correlacionada com o mercado subjacente.
RORAC
Outra medida de avaliação de desempenho extremamente útil é o Return on Risk Adjusted Capital (RORAC), calculado muito simplesmente pelo coeficiente entre a taxa de rendibilidade obtida por um determinado fundo e o respectivo Value-at-Risk, no mesmo período (ver Value-at-Risk).
 |
, sendo Rp a taxa de rendibilidade do fundo p, e VaRp o Value-at-Risk do fundo p. |
A vantagem deste indicador reside na possibilidade de "fugir" ao pressuposto, considerado nos outros indicadores, de que as taxas de rendibilidade seguem uma distribuição aproximadamente normal. Com efeito, este pressuposto para algumas classes de activo e/ou tipo de fundos (e.g, hedge funds) pode ser enganador por subestimar (porventura significativamente) o risco assumido. Ao "trabalhar" com o Value-at-Risk, o RORAC permite assumir distribuições mais ajustadas à realidade, mais defensivas e ajustadas à realidade.
11. Outras condições podem ser utilizadas, como por exemplo, retornos abaixo de um determinado nível, em vez de só os negativos.